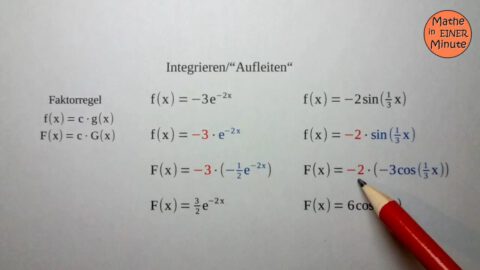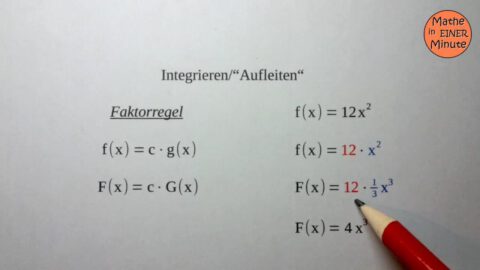188 – Potenzregel beim Bilden von Stammfunktionen – Beispiel
Beispiel zur Anwendung der Potenzregel beim Bestimmen von Stammfunktionen. Mit einem Dezimalbruch (einer Kommazahl) im Exponenten.
187 – Potenzregel beim Bilden von Stammfunktionen – Beispiel
Beispiele für das Bestimmen von Stammfunktionen mithilfe der Potenzregel.
186 – Potenzregel beim Bilden von Stammfunktionen – Verständnis
Verständnis für die Potenzregel beim Bestimmen von Stammfunktionen.
185 – Faktorregel beim Bilden von Stammfunktionen 4 – Beispiel
Beispiel für das Bestimmen von Stammfunktionen mithilfe der Faktorregel.
184 – Faktorregel beim Bilden von Stammfunktionen 3 – Beispiel
Beispiel für das Bestimmen von Stammfunktionen mithilfe der Faktorregel.
183 – Faktorregel beim Bilden von Stammfunktionen 2 – Beispiel
Beispiele für das Bestimmen von Stammfunktionen mithilfe der Faktorregel.
182 – Faktorregel beim Bilden von Stammfunktionen – Beispiel
Beispiele für das Bestimmen von Stammfunktionen mithilfe der Faktorregel.
181 – Faktorregel beim Bilden von Stammfunktionen – Verständnis
Verständnis für die Faktorregel beim Bestimmen von Stammfunktionen.
175 – Summenregel beim Bilden von Stammfunktionen – Verständnis
Verständnis für die Summenregel beim Bestimmen von Stammfunktionen.
173 – Stammfunktion trigonometrischer Funktion / Kettenregel 6 – Beispiel
Bestimmen einer Stammfunktion einer verketteten trigonometrischen Funktion mithilfe der Umkehrung der Kettenregel für Ableitungen.